3. Longest substring

Problem

Given a string s, find the length of the longest substring without duplicate characters.

Example 1

Input: s = "abcabcbb"
Output: 3
Explanation: The answer is "abc", with the length of 3.

Example 2

Input: s = "bbbbb"
Output: 1
Explanation: The answer is "b", with the length of 1.

Example 3

Input: s = "pwwkew"
Output: 3
Explanation: The answer is "wke", with the length of 3.
Notice that the answer must be a substring, "pwke" is a subsequence and not a substring.

Brute Force

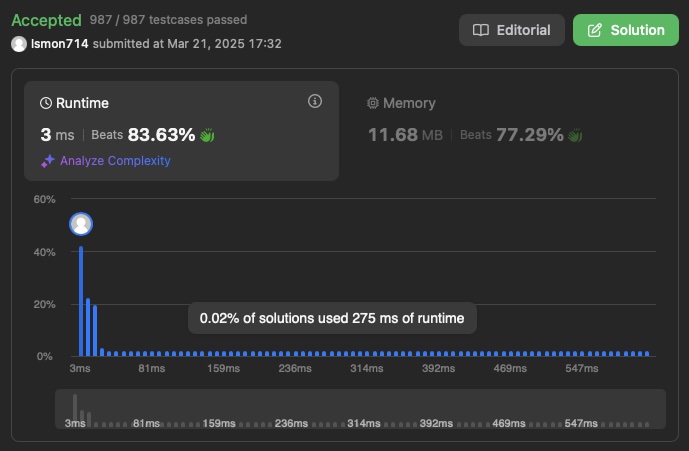
Intuition

I thought of using a sliding window to find duplicates and a map that tracks the precense and position of character

Approach

I thought of using sliding window to find the longest non repeating substring.

1. Initialize 2 pointers (start and end) that mark the range of the sliding window.
2. Iterate throguth the input string s updating the start pointer if we encounter a duplicated character and moving the end pointer processing the next character.
3. After iterating thorugh all characters in the string return the maximum length found during the process.

Time complexity

I believe that the works case scenario can be $O(n^2)$ because not only hast to go through the length of the string but also go through the map I am adding characters each time making it work dobule duty if the map is pretty full.

Space complexity

$O(min(m,n))$ where m is the size of the character set (for example 128 for ASCII) and n which is the length of the string and due to the unordered_map that store characters which stores only unique characters seen in the current window.

Code

class Solution {
public:
    int lengthOfLongestSubstring(string s) {
        if (s.empty()) return 0;

        int start = 0, maxLen = 0;
        unordered_map<char, int> map;
        
        for(int end = 0; end < s.size(); end++) {
            char c = s[end];
            if (map.count(c) && map[c] >= start) {
                start = map[c] + 1;
            } 
            map[c] = end; // Update last position of current character
            maxLen = std::max(maxLen, end - start + 1);
        }
        return maxLen;
    }
};

Optimized approach

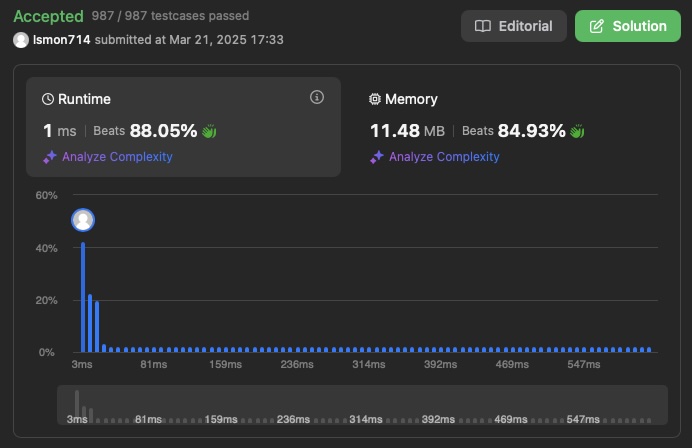
Intuition

Based on my approach on the brute force approach where I used an unordered_map to do the character counting. And thinking I could get eliminate the map using an array representing the 128 charactors of the ASCII code.

Approach

• Terying to reduce the number of map operations
• Using a more space efficent data structure for the characters.
• Minimizing the updates of variables.

1. Array instead of Hash Map:

   • Uses a fixed-size array (128 for ASCII) instead of unordered_map
   • Constant time O(1) lookups vs. average O(1) with potential collisions
   • Less memory overhead

2. Single Pass Efficiency:

   • Eliminates the need for map.count() checks
   • Combines the position check and update in one step
   • Uses array initialization to avoid explicit clearing

3. Reduced Operations:

   • Stores position+1 to avoid adding 1 later
   • Uses running max to avoid recalculation

Time complexity:

Removing worst case scenarios (hash map operations) and having a more constant $O(n)$

Space complexity:

Brute force: $O(min(m, n))$
Now: $O(128)$ (128 ASCI characters) => $O(1)$

Code

class Solution {
public:
    int lengthOfLongestSubstring(string s) {
        if (s.empty()) return 0;
        int lastSeen [128] = {0};
        int maxLen = 0, start = 0;
        for (int end = 0; end < s.size(); end++) {
            start = std::max(start, lastSeen[s[end]]);
            maxLen = std::max(maxLen, end -start + 1);
            lastSeen[s[end]] = end + 1;
        }
        return maxLen;
    }
};