5. longest palindromic substring

Problem

Given a string s, return the longest palindromic substring in s.

Example 1:

Input: s = "babad"
Output: "bab"
Explanation: "aba" is also a valid answer.

Example 2:

Input: s = "cbbd"
Output: "bb"

Constraints:

1 <= s.length <= 1000

s consist of only digits and English letters.

Brute forced and easy solution

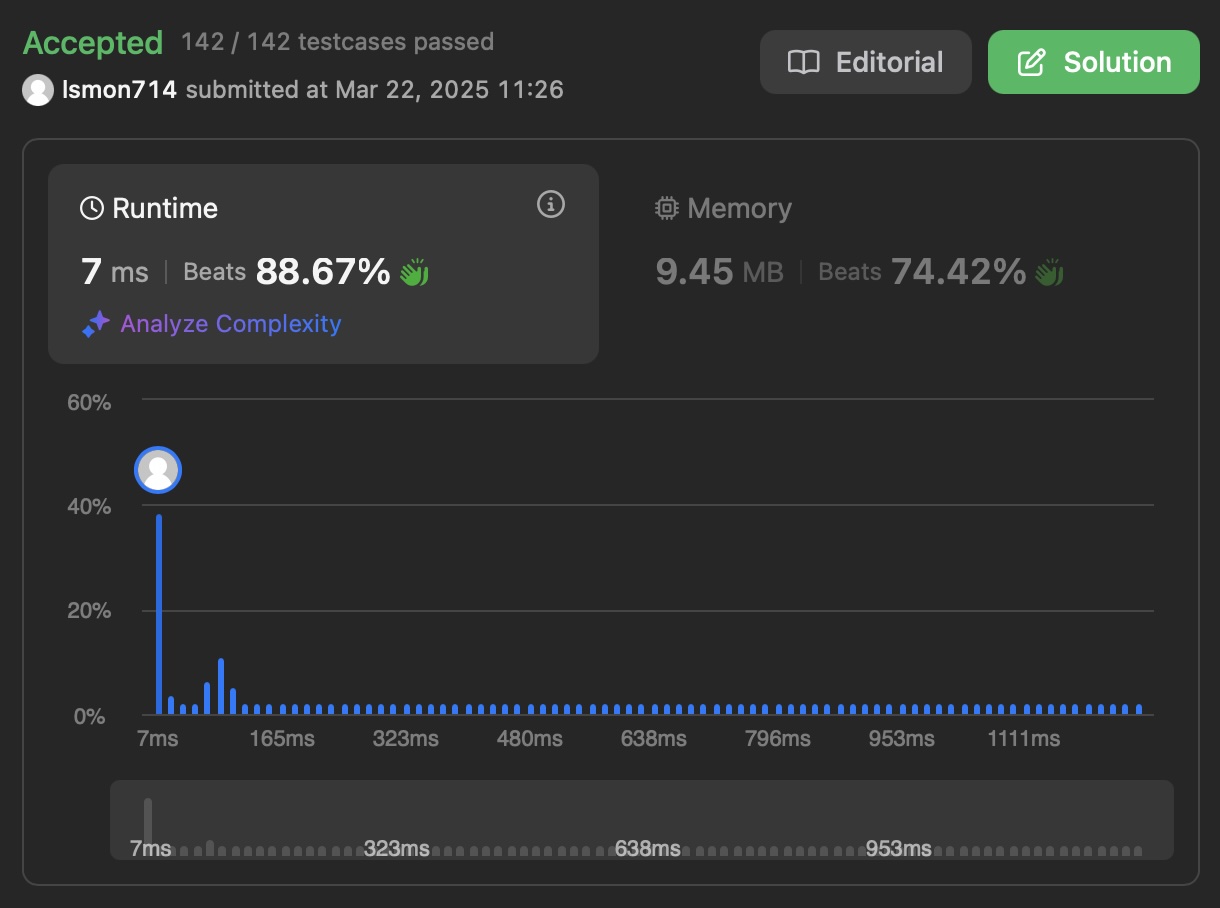
Intuition

To solve the problem of finding the longest palindromic substring in a given string s, we need an efficient approach that works within the constraints: the string length is between 1 and 1000 characters, and it consists only of digits and English letters. A palindrome is a sequence of characters that reads the same forwards and backwards, such as "bab" or "bb", and we are tasked with returning the longest such contiguous substring.

• Substring: A substring is a contiguous sequence of characters in the string. For example, in "babad", "bab" is a substring, but "bbd" is not.

• Palindrome: A palindrome can be of odd length (e.g., "aba" with a single center 'b') or even length (e.g., "bb" with the center between the two 'b's).

• Goal: Among all palindromic substrings, return the one with the maximum length. If multiple palindromes have the same maximum length, any one is acceptable (e.g., in "babad", both "bab" and "aba" are valid outputs).

Approach

A brute-force method—checking all possible substrings and verifying if each is a palindrome—would take ($O(n^3)$ time $O(n^2)$ substrings, $O(n)$ per palindrome check), which is inefficient for n up to 1000. Instead, we use a more efficient strategy based on the symmetry of palindromes: every palindrome has a center, and we can expand outwards from each potential center to find the longest palindrome it forms.

• Two Types of Palindromes:

  • Odd-length: Centered at a single character (e.g., "aba" centered at 'b').
  • Even-length: Centered between two adjacent characters (e.g., "bb" centered between the two 'b's).

• Expansion:

  • For each position i, treat i as the center of an odd-length palindrome and expand outwards.
  • For each pair i and i+1, treat the space between them as the center of an even-length palindrome and expand outwards.

• Efficiency:

  • There are n positions for odd centers and n-1 for even centers, roughly 2n centers total.

Each expansion takes up to $O(n)$ time in the worst case, making the total time complexity $O(n^2)$, or about 1 million operations for n = 1000, which is acceptable.

• Algorithm:
  • Initialize variables to track the starting index (start) and length (max_length) of the longest palindrome found.
  • For each index i from 0 to n-1:
    • Odd-length check: Start with left = i, right = i, and expand while s[left] == s[right] and indices are within bounds.
    • Even-length check: Start with left = i, right = i + 1, and expand similarly.
  • Update start and max_length whenever a longer palindrome is found.
  • Return the substring using the final start and max_length.

Time complexity:

$O(n^2)$. For each of ~2n centers, expansion is $O(n)$.

Space complexity:

$O(1)$. Only a few variables are used, excluding the output string.

Code

class Solution {
public:
    string longestPalindrome(string s) {
        int n = s.length();
        int start = 0;
        int max_length = 1;
        for (int i = 0; i < n; i++) {
            int left = i;
            int right = i;
            while (left >= 0 && right < n && s[left] == s[right]) {
                if (right - left + 1 > max_length) {
                    start = left;
                    max_length = right - left + 1;
                }
                left--;
                right++;
            }
            left = i;
            right = i + 1;
            while (left >= 0 && right < n && s[left] == s[right]) {
                if (right - left + 1 > max_length) {
                    start = left;
                    max_length = right - left + 1;
                }
                left--;
                right++;
            }
        }
        return s.substr(start, max_length);
    }
};

---

Optimized and hard solution (After sking AI)

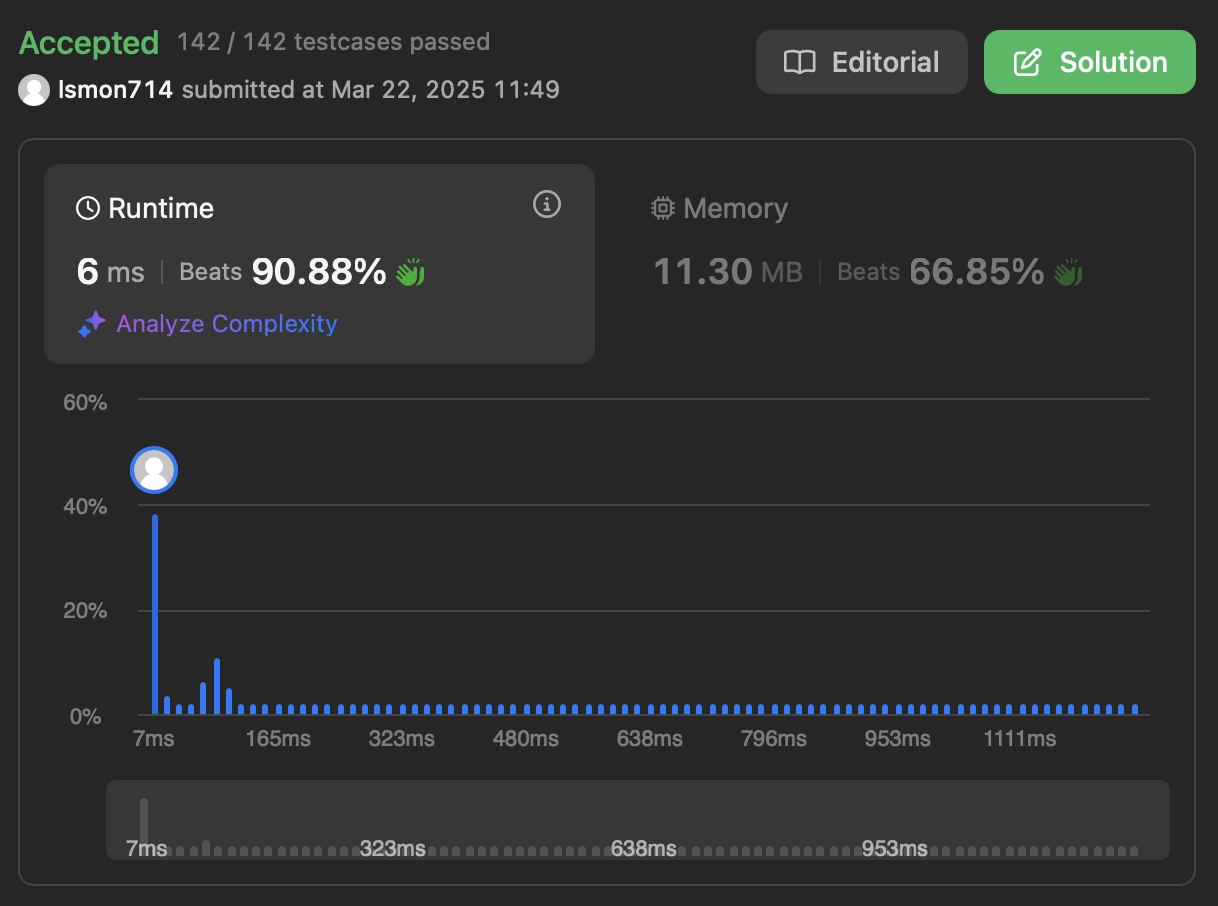
Intuition

To find the longest palindromic substring in a string efficiently, an optimized solution is to use Manacher’s Algorithm, which runs in O(n) time complexity, where n is the length of the input string. This is a significant improvement over the more straightforward O(n²) approaches, especially for larger strings. Below, I’ll explain the algorithm step-by-step and provide a complete solution with example code.

Approach

Manacher’s Algorithm is designed specifically to find the longest palindromic substring by exploiting the symmetry of palindromes. Here’s how it works:

Key Concepts:

1. Palindrome Symmetry: Palindromes are symmetric around their center. The algorithm uses this property to reuse previously computed palindrome lengths, avoiding redundant character comparisons.
2. Transformed String: To handle both odd-length (e.g., "aba") and even-length (e.g., "bb") palindromes uniformly, the input string is preprocessed by inserting special characters (e.g., #) between each character and at the boundaries. For example, "babad" becomes #b#a#b#a#d#.
3. Palindrome Radii Array: An array P is maintained, where P[i] represents the radius of the palindrome centered at position i in the transformed string. The radius is the number of characters on either side of the center that match.
4. Center and Right Boundary: The algorithm tracks the current center C of a palindrome and its rightmost boundary R. For a new position i, it uses the symmetry around C to initialize P[i] and then expands only when necessary.

Steps:

1. Preprocess the String: Transform the input string by adding special characters (e.g., #) to make all palindromes odd-length in the transformed string.

2. Compute Palindrome Radii:

   • For each position i, initialize P[i] using the mirror property if i is within R.
   • Expand around i to verify and extend the palindrome, updating P[i].
   • Adjust C and R if the palindrome at i extends beyond the current R.

3. Find the Longest Palindrome: Track the maximum value in P and its corresponding center, then map it back to the original string.

Complexity

• Time complexity:

The transformation takes $O(n)$, and the main loop processes each character in amortized $O(1)$ time due to the mirror property and bounded expansions.

• Space complexity:

Space is used for the transformed string and the P array, both of which are proportional to the input size.

Code

#include <string>
#include <vector>
#include <algorithm>
using namespace std;

class Solution {
public:
    string longestPalindrome(string s) {
        int n = s.length();
        if (n <= 1) return s; // Handle empty or single-character strings

        // Step 1: Transform the string
        string transformed = "#";
        for (char c : s) {
            transformed += c;
            transformed += "#";
        }
        int t_len = transformed.length();

        // Step 2: Initialize the palindrome radii array and variables
        vector<int> P(t_len, 0); // P[i] = radius of palindrome centered at i
        int C = 0; // Current center
        int R = 0; // Right boundary of the palindrome centered at C
        int max_len = 0; // Length of the longest palindrome
        int center_index = 0; // Center of the longest palindrome

        // Step 3: Compute palindrome radii for each position
        for (int i = 0; i < t_len; i++) {
            // Use mirror property if i is within R
            int mirr = 2 * C - i; // Mirror position of i around C
            if (i < R) {
                P[i] = min(R - i, P[mirr]);
            }

            // Expand around i to find the full palindrome
            int left = i - (1 + P[i]);
            int right = i + (1 + P[i]);
            while (left >= 0 && right < t_len && transformed[left] == transformed[right]) {
                P[i]++;
                left--;
                right++;
            }

            // Update C and R if the palindrome extends beyond R
            if (i + P[i] > R) {
                C = i;
                R = i + P[i];
            }

            // Track the longest palindrome
            if (P[i] > max_len) {
                max_len = P[i];
                center_index = i;
            }
        }

        // Step 4: Extract the substring from the original string
        int start = (center_index - max_len) / 2; // Map back to original string
        return s.substr(start, max_len);
    }
};